5.6 如何寻找最长回文子串

本文对应的力扣题目：

5.最长回文子串

string longestPalindrome(string s) {
    string res;
    for (int i = 0; i < s.size(); i++) {
        // 寻找长度为基数的回文子串
        string s1 = palindrome(s, i, i);
        // 寻找长度为偶数的回文子串
        string s2 = palindrome(s, i, i + 1);
        // res = longest(res, s1, s2)
        res = res.size() > s1.size() ? res : s1;
        res = res.size() > s2.size() ? res : s2;
    }
    return res;
}

// 从 s[l] 和 s[r] 开始向两端扩散
// 返回以 s[l] 和 s[r] 为中心的最长回文串
string palindrome(string& s, int l, int r) {
    // 防止索引越界
    while (l >= 0 && r < s.size() && s[l] == s[r]) {
        l--; r++;
    }
    return s.substr(l + 1, r - l - 1);
}

var longestPalindrome = function(s) {
    // 初始化左右指针
    let l = 0, r = 0;
    let n = s.length;
    // 如果只有一个字符的回文串，直接返回
    if(n < 2)  return s;
    // 开始遍历
    for(let i = 0; i <= n; i++){
        // 如果回文串长度是奇数,取中间字符
        palindrome(i, i)
        // 如果回文串长度是偶数，取相邻字符
        palindrome(i, i+1)
    }
    function palindrome(z, y){
        // 当左指针z >= 0 && 右指针y < 回文串长度n && 左指针z === 右指针y
        while(z >=0 && y < n && s[z] == s[y]){
            z--
            y++
        }
        // 如果此轮询长度 大于 之前记录长度
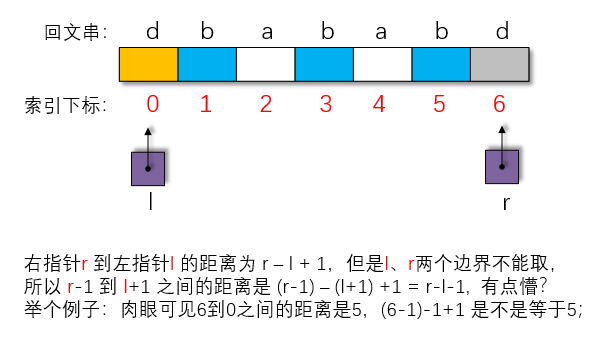
        // 此时y到z之间的距离是 y-z+1, 但是又不能取边界，
        // 所以 y-1 到 z+1 之间的距离是 (y-1)-(z+1)+1 = y-
        if(y-z-1 > r-l-1){
            l=z
            r=y
        }
    }
    // 返回新数组，左指针不包含0位字符
    return s.slice(l+1, r)
};